Filtri Elettronici Attivi e Passivi: 6 + 1 esempi applicativi

Boardesign, 24/03/2025
Cosa sono i filtri in elettronica?
I filtri elettronici sono componenti fondamentali nei sistemi di elaborazione dei segnali. La loro funzione principale è quella di modificare selettivamente le componenti in frequenza di un segnale, permettendo il passaggio di alcune frequenze mentre ne attenuano altre. Questa caratteristica li rende strumenti essenziali in numerose applicazioni, dalle telecomunicazioni all’audio, dall’elettronica di consumo ai sistemi di controllo industriale.
Filtri attivi e passivi
A seconda di come vengono realizzati, i filtri possono essere attivi o passivi. I filtri attivi assumono una particolare importanza grazie alla loro capacità di migliorare significativamente le prestazioni rispetto ai più tradizionali filtri passivi.
I filtri attivi si distinguono dai filtri passivi perché, oltre a utilizzare componenti passivi come resistori e condensatori, impiegano anche componenti attivi quali amplificatori operazionali (op-amp) o amplificatori a transconduttanza operazionale (OTA). Grazie a questi componenti, i filtri attivi offrono prestazioni migliorate, come guadagno regolabile, alta impedenza di ingresso, bassa impedenza di uscita e maggiore selettività.
Tipologie di Filtri in Base alla Risposta in Frequenza
I filtri si distinguono principalmente in base alla loro risposta in frequenza, ben rappresentata tramite il diagramma di Bode (nelle figure seguenti non viene rappresentata la fase del segnale):
- Filtri passa-basso (Low-Pass Filter, LPF): Permettono il passaggio delle frequenze inferiori a una frequenza detta frequenza di taglio (fc), attenuando le componenti a frequenza più elevata. Sono utilizzati per eliminare il rumore ad alta frequenza o per estrarre la componente continua di un segnale.
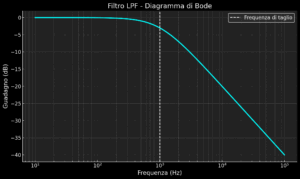
- Filtri passa-alto (High-Pass Filter, HPF): Complementari ai passa-basso, consentono il passaggio delle frequenze superiori alla frequenza di taglio, attenuando quelle inferiori. Vengono impiegati per eliminare offset o deriva di componenti continue.
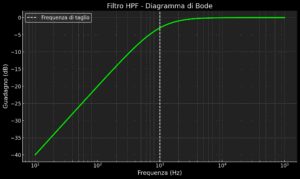
- Filtri passa-banda (Band-Pass Filter, BPF): Permettono il passaggio solo delle frequenze comprese in un determinato intervallo, attenuando sia le frequenze inferiori che quelle superiori. Sono fondamentali nei ricevitori radio per selezionare un canale specifico.
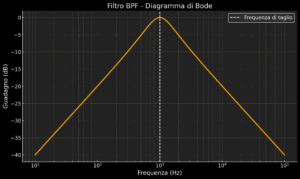
- Filtri elimina-banda (Notch Filter): Attenuano le frequenze in un intervallo specifico, lasciando passare sia le frequenze inferiori che quelle superiori. Vengono utilizzati per eliminare interferenze a frequenze note, come il rumore di rete a 50/60 Hz. Filtro notch: Variante del filtro elimina-banda con una banda di reiezione estremamente stretta. Ideale per eliminare interferenze precise, come quelle a 50 o 60 Hz tipiche dell’alimentazione elettrica.
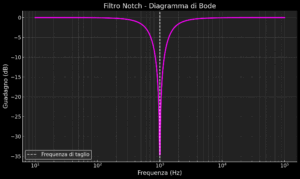
- Filtro all-pass: Non modifica l’ampiezza delle frequenze, ma altera la relazione di fase tra esse. Utile in applicazioni in cui è fondamentale correggere le distorsioni di fase
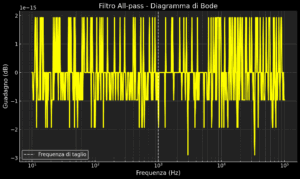
Ordine del Filtro: Una Questione di Poli e Zeri
L’ordine di un filtro è un parametro associato alla “ripidità” della transizione tra la banda passante e la banda attenuata. Matematicamente, l’ordine corrisponde al grado del polinomio che descrive la funzione di trasferimento del filtro e in particolare è legato al numero di poli e zeri del polinomio. Più alto è l’ordine, maggiore è il numero di poli e più ripida è la transizione tra banda passante (frequenze lasciate passare) e banda di reiezione (frequenze attenuate). In alcuni casi, possono esserci anche degli zeri nella funzione di trasferimento, che rappresentano frequenze dove il segnale viene completamente annullato.
In sintesi:
- I poli determinano la rapidità della caduta del segnale nella zona di transizione.
- Gli zeri definiscono la presenza di punti in cui il segnale viene completamente eliminato o fortemente attenuato.
Un filtro del primo ordine presenta un’attenuazione di 20 dB per decade (o 6 dB per ottava) nella banda di transizione. Ogni ordine aggiuntivo aumenta questa attenuazione di ulteriori 20 dB per decade. Ad esempio, un filtro del secondo ordine avrà un’attenuazione di 40 dB per decade (12 dB per ottava).
Filtri di ordine superiore offrono transizioni più nette tra banda passante e banda attenuata, ma presentano maggiore complessità circuitale e possono introdurre distorsioni di fase più significative. La scelta dell’ordine del filtro rappresenta quindi un compromesso tra prestazioni e complessità implementativa.
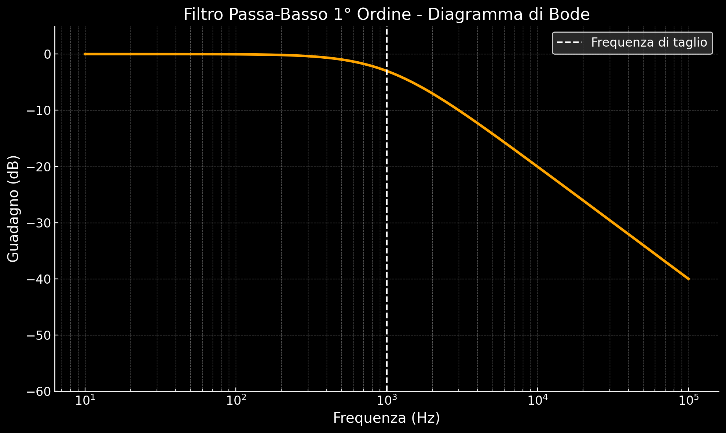
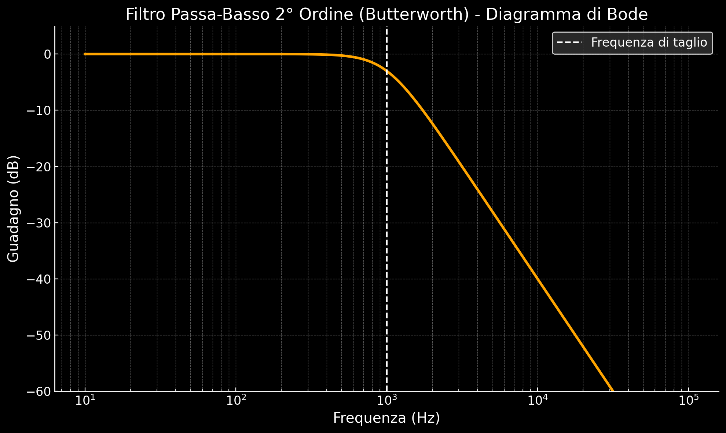
Differenza dell’attenuazione in un filtro LPF del primo ordine (a sinistra) e del secondo ordine (a destra)
Un Parametro Misterioso: Q
Il fattore Q di un filtro definisce la selettività e l’ampiezza della banda attorno alla frequenza centrale del filtro. Costituisce sostanzialmente un fattore di qualità: un valore elevato di Q indica una banda passante più stretta e una maggiore selettività, mentre un valore basso corrisponde a una banda più ampia e a una minore selettività. È essenziale per determinare la risposta del filtro, la sua capacità di isolare frequenze specifiche e per gestire eventuali risonanze indesiderate. Matematicamente, il fattore di qualità (Q) di un filtro è definito come il rapporto tra la frequenza centrale (f0) e la larghezza della banda passante (Δf), cioè: 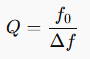
Metodi di Filtraggio Passivi
1. Filtro RC
Il filtro RC passa-basso rappresenta la soluzione più semplice ed economica per implementare un filtraggio in frequenza. È composto da un resistore (R) e un condensatore (C) collegati in serie, con l’uscita prelevata ai capi del condensatore.
Funzionamento: A basse frequenze, il condensatore si comporta come un circuito aperto, permettendo al segnale di passare. All’aumentare della frequenza, l’impedenza del condensatore diminuisce, cortocircuitando progressivamente il segnale verso massa.
Vantaggi:
- Semplicità costruttiva e basso costo
- Assenza di alimentazione esterna (passivo)
- Affidabilità elevata
- Dimensioni ridotte
Svantaggi:
- Filtro solo del primo ordine (20 dB/decade)
- Frequenza di taglio dipendente dal carico
- Impedenza di uscita non costante
- Attenuazione anche nella banda passante
Applicazione pratica: Nei circuiti audio, per eliminare il rumore ad alta frequenza prima della conversione analogico-digitale. Ad esempio, negli ingressi microfonici di registratori digitali, un filtro RC con frequenza di taglio intorno ai 20 kHz permette di eliminare le interferenze ultrasoniche preservando l’intero spettro audio udibile.
2. Filtro LC Passa-Banda
I filtri LC sfruttano la combinazione di induttori (L) e condensatori (C) per creare circuiti risonanti in grado di selezionare bande di frequenza specifiche.
Funzionamento: Un circuito LC presenta una risonanza alla frequenza determinata da f = 1/(2π√(LC)). A questa frequenza, le impedenze di induttore e condensatore si annullano a vicenda, permettendo al segnale di passare con minima attenuazione.
Vantaggi:
- Possibilità di realizzare filtri del secondo ordine e superiori
- Migliore selettività rispetto ai filtri RC
- Basse perdite nella banda passante
- Capacità di gestire potenze elevate
Svantaggi:
- Dimensioni maggiori rispetto ai filtri RC
- Sensibilità ai campi magnetici esterni
- Componenti induttivi più costosi e meno precisi
- Possibile presenza di risonanze parassite
Applicazione pratica: Nei ricevitori radio, dove i filtri LC vengono utilizzati come “frontend” per selezionare la banda di frequenza desiderata. Ad esempio, in un ricevitore AM, un filtro LC sintonizzato sulla frequenza della stazione desiderata (es. 1 MHz) permette di separare il segnale di interesse da altre trasmissioni adiacenti.
3. Filtri a Cristallo
I filtri a cristallo rappresentano una soluzione passiva più sofisticata, basata sulle proprietà piezoelettriche di cristalli di quarzo o ceramiche speciali.
Funzionamento: Sfruttano il fenomeno della risonanza meccanica dei cristalli, che si manifesta elettricamente come un circuito risonante ad altissimo fattore di qualità (Q). Ciò consente di ottenere bande passanti estremamente strette e ripide.
Vantaggi:
- Elevatissima selettività (fattore Q fino a 100.000)
- Eccellente stabilità in frequenza al variare della temperatura
- Ottima ripetibilità delle caratteristiche
- Dimensioni contenute rispetto a filtri LC equivalenti
Svantaggi:
- Costo elevato per design personalizzati
- Limitata capacità di gestione della potenza
- Banda passante relativamente fissa (difficile da regolare)
- Gamma di frequenze limitata (tipicamente kHz-MHz)
Applicazione pratica: Nei sistemi di comunicazione digitale, come modem e ricevitori GPS, dove è necessaria un’elevata selettività per separare canali adiacenti. Ad esempio, nei ricevitori di comunicazioni satellitari professionali, filtri a cristallo con larghezza di banda di pochi kHz permettono di isolare con precisione i canali di comunicazione anche in presenza di segnali interferenti molto vicini in frequenza.
Metodi di Filtraggio Attivi
4. Filtri Attivi basati su Amplificatori Operazionali
I filtri attivi integrano componenti passivi (resistori e condensatori) con amplificatori operazionali (op-amp), permettendo di superare molte limitazioni dei filtri puramente passivi.
Funzionamento: Gli amplificatori operazionali forniscono guadagno e isolamento tra gli stadi, permettendo di concatenare più sezioni di filtraggio senza effetti di carico reciproco. Le topologie più comuni includono Sallen-Key, Multiple Feedback e State Variable.
Vantaggi:
- Possibilità di implementare facilmente filtri di ordine elevato
- Assenza di componenti induttivi (problematici in termini di costo e dimensioni)
- Impedenza di ingresso elevata e di uscita bassa
- Possibilità di integrare funzioni di guadagno e filtraggio
Svantaggi:
- Necessità di alimentazione esterna
- Limitazioni in frequenza dovute alla banda degli op-amp
- Sensibilità al rumore introdotto dagli amplificatori
- Distorsione potenziale per segnali di grande ampiezza
Applicazione pratica: Nei sistemi di acquisizione dati industriali, dove i filtri anti-aliasing sono cruciali prima della conversione analogico-digitale. Ad esempio, in un sistema di monitoraggio di vibrazioni, un filtro attivo Butterworth del 4° ordine con frequenza di taglio a 1 kHz assicura che i segnali ad alta frequenza non causino errori di campionamento, mantenendo al contempo una risposta in fase lineare nella banda di interesse.
5. Filtri Attivi gm-C (Transconduttanza-C)
I filtri gm-C integrano condensatori con amplificatori operazionali a transconduttanza (OTA) per creare circuiti di filtraggio particolarmente adatti alle applicazioni ad alta frequenza e integrazioni in circuiti integrati.
Funzionamento: Gli OTA convertono la tensione in ingresso in una corrente proporzionale (transconduttanza). Questa corrente pilotata carica e scarica i condensatori creando una risposta in frequenza regolabile elettronicamente tramite la modifica della transconduttanza degli OTA stessi. Ciò permette una facile variazione della frequenza di taglio semplicemente modificando una corrente di polarizzazione o una tensione di controllo.
Vantaggi:
- Possibilità di funzionamento ad alta frequenza (MHz e GHz)
- Controllo elettronico preciso della frequenza di taglio
- Alta integrabilità in tecnologia CMOS e BiCMOS
- Assenza totale di componenti induttivi
- Elevata impedenza d’ingresso e buona capacità di pilotaggio dei carichi
Svantaggi:
- Sensibilità alle non linearità e alle variazioni parametriche degli OTA
- Complessità progettuale, specialmente nella gestione delle non idealità
- Possibili problemi di stabilità e oscillazioni indesiderate se non correttamente progettato
- Maggiore sensibilità al rumore rispetto ad altre soluzioni attive
Applicazione pratica: I filtri gm-C sono particolarmente utilizzati nei sistemi di comunicazione wireless, come ricevitori RF e filtri selettivi programmabili, dove è fondamentale variare elettronicamente la banda passante e adattarsi rapidamente a diversi standard di comunicazione. Un esempio concreto è un ricevitore radio software-defined (SDR), dove un filtro gm-C permette di selezionare con precisione e rapidità il canale operativo, mantenendo basse perdite di segnale e alta selettività.
6. Filtri Wave Active (WAF)
I filtri Wave Active simulano i tradizionali filtri passivi LC (ladder) utilizzando una rete di componenti attivi come amplificatori operazionali, resistori e condensatori. Sono particolarmente indicati per applicazioni che richiedono elevata precisione e stabilità nel tempo.
Funzionamento: I filtri WAF emulano il comportamento dei filtri LC tramite amplificatori operazionali configurati per simulare le funzioni di trasferimento tipiche delle reti passive LC. Ogni stadio attivo è progettato per replicare specifiche risposte in frequenza, consentendo così di ottenere facilmente filtri complessi di ordine elevato con prestazioni stabili e precise.
Vantaggi:
- Stabilità e precisione della risposta in frequenza, meno influenzata da variazioni termiche e tolleranze dei componenti
- Bassa sensibilità alle variazioni parametriche
- Eccellente linearità e basso rumore
- Facilità nella realizzazione di filtri complessi ad alto ordine senza componenti induttivi
Svantaggi:
- Elevata complessità circuitale che richiede una progettazione più accurata
- Necessità di un numero considerevole di componenti attivi e passivi
- Maggiore ingombro e costo rispetto ad altri tipi di filtri attivi
- Potenziali problemi di stabilità se la rete attiva non è adeguatamente compensata
Applicazione pratica: I filtri WAF trovano ampio impiego nei sistemi di acquisizione dati e strumentazione di precisione, come analizzatori di spettro, strumenti di misura ad alta risoluzione e apparecchiature biomedicali. Ad esempio, in un sistema di acquisizione dati per test di laboratorio, un filtro Wave Active di alto ordine garantisce che il segnale acquisito sia libero da interferenze e rumori ambientali, mantenendo elevata stabilità nel tempo e consentendo misurazioni affidabili e ripetibili.
Una via differente: I Filtri Digitali
I filtri digitali rappresentano l’approccio più avanzato e flessibile al filtraggio, implementando algoritmi matematici su dati già convertiti in formato digitale. Vengono implementati su microcontrollori, microprocessori, DSP (Digital Signal Processor) e FPGA (Field Programmable Gate Array) che abbiano sufficiente potenza di calcolo per implementarli.
Funzionamento: Elaborano sequenze di campioni numerici applicando operazioni matematiche (moltiplicazioni e somme) secondo coefficienti predeterminati. Si dividono principalmente in filtri a risposta impulsiva finita (FIR) e a risposta impulsiva infinita (IIR).
Vantaggi:
- Estrema flessibilità e riconfigurabilità via software
- Precisione e ripetibilità eccellenti
- Possibilità di implementare funzioni di trasferimento complesse
- Stabilità garantita (nei filtri FIR)
- Assenza di deriva dei componenti nel tempo
Svantaggi:
- Necessità di conversione analogico-digitale
- Latenza di elaborazione
- Limitazioni di banda dovute alla frequenza di campionamento
- Requisiti computazionali potenzialmente elevati
- Possibili problemi di quantizzazione e overflow
Applicazione pratica: Nell’elaborazione audio professionale, dove i filtri digitali consentono operazioni di equalizzazione parametrica estremamente precise. Ad esempio, in un sistema di cancellazione del rumore adattiva, filtri digitali FIR con centinaia di coefficienti permettono di identificare e rimuovere selettivamente rumori ambientali preservando la qualità del parlato, con applicazioni che spaziano dalle telecomunicazioni ai sistemi di riconoscimento vocale in ambienti industriali rumorosi.
Confronti e Conclusioni
| Metodo di Filtraggio | Complessità | Ordine Tipico | Selettività | Flessibilità | Costo | Applicazioni Tipiche |
| Filtro RC Passivo | Molto bassa | 1° ordine | Bassa | Limitata | Molto basso | Deaccoppiamento DC, pre-filtri audio |
| Filtro LC Passivo | Media | 2°-4° ordine | Media | Media | Medio | Ricevitori radio, crossover audio |
| Filtro a Cristallo | Media | Elevato (Q>1000) | Molto alta | Bassa | Alto | Comunicazioni RF, oscillatori |
| Filtro Attivo (Op-Amp) | Media-alta | 2°-8° ordine | Alta | Alta | Medio | Strumentazione, audio hi-fi |
| Filtri gm-C (OTA) | Alta | 2° – 6° | Alta | Alta | Medio-alto | Comunicazioni wireless, ricevitori RF |
| Filtri Wave Active (WAF) | Alta | 3° – 10° | Molto Alta | Media | Alto | Acquisizione dati, strumentazione di laboratorio |
| Filtro Digitale | Alta | Virtualmente illimitato | Eccellente | Eccellente | Alto (hardware) Basso (software) | DSP, telecomunicazioni, multimedia |
Questa panoramica sulle tecniche di filtraggio mette in evidenza la grande diversità di approcci disponibili per affrontare efficacemente le esigenze sempre più sofisticate dei sistemi elettronici moderni. Dai semplici e affidabili filtri RC passivi, ideali per applicazioni basilari e a basso costo, fino ai complessi filtri digitali capaci di offrire precisione assoluta e massima flessibilità operativa, ciascun metodo presenta caratteristiche uniche che lo rendono più o meno adatto a specifici scenari applicativi.
I filtri passivi, come i filtri RC, LC e i filtri a cristallo, offrono semplicità senza la necessità di alimentazione esterna, risultando ideali nei circuiti elettronici dove siano necessari compattezza e basso costo e dove non occorrano prestazioni molto elevate. Tuttavia, dimensioni degli elementi induttivi, derive termiche e temporali e limitazioni nelle prestazioni, li rendono meno flessibili rispetto alle soluzioni attive.
I filtri attivi, inclusi quelli basati su amplificatori operazionali (Sallen-Key, Multiple Feedback), OTA (gm-C) e Wave Active Filters (WAF), consentono di superare molte delle limitazioni delle soluzioni passive. Offrono una maggiore versatilità, la possibilità di configurare facilmente filtri di ordine elevato e un controllo più accurato delle prestazioni tramite regolazioni elettroniche. Questi filtri risultano essenziali in strumentazione, acquisizione dati e applicazioni audio e RF di precisione.
Infine, i filtri digitali rappresentano la massima espressione di flessibilità, riconfigurabilità e precisione, permettendo implementazioni virtualmente illimitate in termini di ordine, risposta e adattamento in tempo reale alle condizioni operative. Nonostante ciò, richiedono conversione analogico-digitale e potenza di calcolo, che li rendono ideali prevalentemente per sistemi avanzati e ad alte prestazioni.
La scelta della tecnica di filtraggio dipende quindi da un’attenta analisi dei requisiti tecnici, economici e applicativi. Una comprensione approfondita delle peculiarità di ogni tipologia di filtro permette di progettare sistemi elettronici ottimizzati, capaci di garantire prestazioni eccellenti e affidabilità nel tempo.
BOARDESIGN è pronta a supportare ogni cliente nella selezione, progettazione e simulazione dei filtri più adeguati alle esigenze specifiche dei propri progetti.
Per Approfondire
- Sedra, Adel S., Smith, Kenneth C., “Microelectronic Circuits”, Oxford University Press (Approfondimento sui filtri attivi con Op-Amp e OTA)
- Van Valkenburg, M.E., “Analog Filter Design”, Oxford University Press (Riferimento dettagliato sulla progettazione di filtri analogici passivi e attivi)
- Huelsman, L.P., Allen, P.E., “Introduction to the Theory and Design of Active Filters”, McGraw-Hill Education (Guida approfondita sulla teoria e progettazione di filtri attivi avanzati)


